Answer:
The dimensions of the sandbox will be 15 feet by 8 feet.
Explanation:
Suppose we want to build a rectangular sandbox where the width is 7 less than the length and the diagonal is 2 feet longer than the length.
If x is the length and y is the width in feet, then we have the equations
x - y = 7 ......... (1) and
 ........ (2)
........ (2)
Now, solving equations (1) and (2) we get
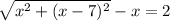
⇒
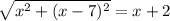
Now, squaring both sides we get,
x² + x² - 14x + 49 = x² + 4x + 4
⇒ x² - 18x + 45 = 0
⇒ (x - 15)(x - 3) = 0
⇒ x = 15 or 3
But from equation (1) x ≠ 3, then x = 15 and y = x - 7 = 8
Therefore, the dimensions of the sandbox will be 15 feet by 8 feet. (Answer)