Question

A satellite is in a circular orbit around the Earth at an altitude of 2.30 106 m. (a) Find the period of the orbit. 2.23 Correct: Your answer is correct. h (b) Find the speed of the satellite. 6.78 Correct: Your answer is correct. km/s (c) Find the acceleration of the satellite. 5.3 Correct: Your answer is correct. m/s2 toward the center of the Earth Need Help? Read It

Answer 1

(a) T = 2.23h

(b) v = 6.78 km/s

(c) a = 5.31 m/s²

Step-by-step explanation:

(a) The period (T) of the orbit can be calculated using Kepler's Third Law equation:

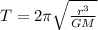`T = 2\pi \sqrt (r^(3))/(GM)` (1)

where r: is the distance from the center of the Earth and the satellite, G: is the gravitational constant = 6.67x10⁻¹¹m³kg⁻¹s⁻² and M: is the Earth's mass = 5.97x10²⁴kg

Since
`r = r_(E) + r_(S) = 6.36\cdot 10^(6)m + 2.30\cdot 10^(6)m = 8.66\cdot 10^(6)m`

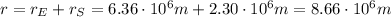
where
`r_(E)`: is the Earth's radius and
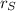`r_(S)`: is the distance between the surface of the Earth and the satellite

Hence, by entering the radius calculated into equation (1) we can find the period of the orbit:

`T = 2\pi \sqrt ((8.66\cdot 10^(6)m)^(3))/(6.67\cdot 10^(-11)m^(3)/kgs^(2)\cdot 5.97\cdot 10^(24)kg) = 8024.3s = 2.23h`

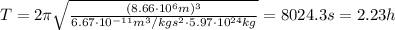
(b) The speed (v) of the satellite can be calculated using the following equation:

`v = \sqrt (GM)/(r) = \sqrt (6.67\cdot 10^(-11)m^(3)/kgs^(2) \cdot 5.97\cdot 10^(24)kg)/(8.66 \cdot 10^(6)m) = 6.78km/s`

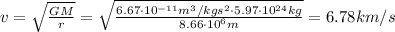
(c) The acceleration (a) of the satellite is:

`a = (v^(2))/(r) = ((6.78 \cdot 10^(3)m/s)^(2))/(8.66\cdot 10^(6)m) = 5.31m/s^(2)`

I hope it helps you!