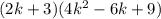Question

Factor 8k3 + 27 by using an identity.
how to do it?

Answer 1

The given expression is factored into
`(2k+3)(4k^2-6k+9)`

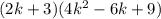
Explanation:

Given:

The expression to factor is given as:

`8k^3+27`

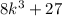
We observe that 8 =
`2* 2* 2=2^3`

Also,
`27 = 3* 3* 3=3^3`

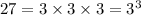
So, the above expression can be rewritten as:

`(2k)^3+3^3`

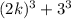
The above expression is of the form
`a^3+b^3`.

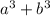We know that the above identity is factored as:

`a^3+b^3=(a+b)(a^2-ab+b^2)`

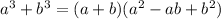
Here,
`a=2k\ and\ b=3`

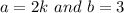
Therefore, the given expression can be factored using the above identity and is factored as:

`(2k)^3+3^3=(2k+3)((2k)^2-(2k)(3)+3^2)\\\\(2k)^3+3^3=(2k+3)(4k^2-6k+9)`

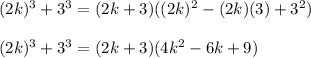
Hence, the given expression is factored into
`(2k+3)(4k^2-6k+9)`