The recursive definition used to generate the sequence {3, 6, 3, 6, 3,...} is:
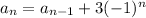 where
where
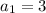 and
and
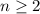
Solution:
Given sequence is 3, 6, 3, 6, 3,...
To find: recursive definition for the sequence
First term in the sequence is 3
Then you add on 3 to get to 6 as the second term
Then add -3 to get 3 as third term
This pattern goes on forever
3 + 3 = 6
6 - 3 = 3
3 + 3 = 6
6 - 3 = 3
and so on
So we can generate a recursive definition as:
Let
 be the nth term and "n" denotes the term's location
be the nth term and "n" denotes the term's location
 is the first term of sequence
is the first term of sequence
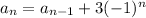 , where
, where
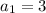 and
and
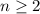
Here,
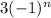 is used to denote , we add on either +3 or -3 to the previous term to get next term
is used to denote , we add on either +3 or -3 to the previous term to get next term