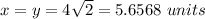Question

Solve for x and y in the given the 45° - 45° - 90° triangle shown above. When applicable, simplify all radicals and show your work.

Answer 1

Therefore,

`x=y= 4√(2)=5.6568\ units`

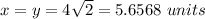
Explanation:

Given:

Consider In Right Angle Triangle ABC

∠B = 90°

∠C = ∠A = 45°

AB = y

BC = x = adjacent side

AC = 8 = hypotenuse

To Find:

x = ?

y = ?

Solution:

In Right Angle Triangle ABC by Cosine Identity we have

`\cos C = \frac{\textrm{side adjacent to angle C}}{Hypotenuse}\\`

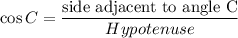
substituting the above given values we get

`\cos 45 = (BC)/(AC)=(x)/(8)`

`(1)/(√(2) ) =(x)/(8)\\\therefore x=(8)/(√(2) ) \\Rationalizing\ we\ get\\\therefore x=(8)/(√(2))* (√(2) )/(√(2))}\\\therefore x=4√(2)=4* 1.4142=5.6568\ units`

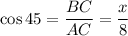
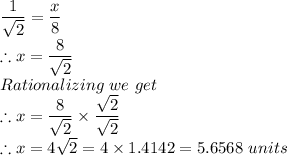
As The triangle is 45 - 45 - 90

It is an Isosceles Right triangle

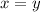`x=y`..... Isosceles Triangle property

`\therefore y=4√(2)=4* 1.4142=5.6568\ units`

Therefore,

`x=y= 4√(2)=5.6568\ units`