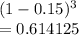Question

Consider a manufacturing process with a quality inspection station. In the past, 15% of parts are defective. As soon as one defective part is found, the process is stopped. If 8 parts have been inspected without finding a defective part, what is the probability that at least 11 total parts will be inspected before the process is stopped?

Answer 1

0.614125

Explanation:

Given that a manufacturing process with a quality inspection station has on an average 15% of parts are defective.

As soon as one defective part is found, the process is stopped.

We find that number of defectives would be binomial because each part randomly selected has a constant probability of 0.15 being defective

Probability that at least 11 total parts will be inspected before the process is stopped/8 parts have been inspected without finding a defective part

=
`P(x\geq 11)/P(x=8)\\`

= Probability of 9th, 10th, 11th should not be defective

=
`(1-0.15)^3\\= 0.614125`