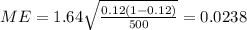Question

A magazine provided results from a poll of 500 adults who were asked to identify their favorite pie. Among the 500 ​respondents, 12 ​% chose chocolate​ pie, and the margin of error was given as plus or minus 5 percentage points. What values do ModifyingAbove p with caret ​, ModifyingAbove q with caret ​, ​n, E, and p​ represent? If the confidence level is 90 ​%, what is the value of alpha ​?

Answer 1

n=500 represent the random sample taken

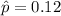`\hat p=0.12` estimated proportion of people that chose chocolate​ pie

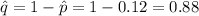`\hat q =1-\hat p=1-0.12=0.88` represent the people that NOT chose chocolate​ pie

E=0.05 represent the error or margin of error given by the following formula:

`ME=z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

p= true population proportion of people that chose chocolate​ pie

If the confidence level is 90 ​%, what is the value of alpha ​?

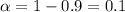`\alpha=1-0.9 =0.1` and the value of
`\alpha/2 =0.05`,

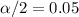`z_(\alpha/2)=-1.64` and
`z_(1-\alpha/2)=1.64`

`ME=1.64 \sqrt{(0.12(1-0.12))/(500)}=0.0238`

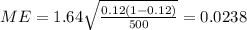
Explanation:

Data given and notation

What values do ModifyingAbove p with caret ​, ModifyingAbove q with caret ​, ​n, E, and p​ represent?

n=500 represent the random sample taken

X represent the people that chose chocolate​ pie

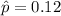`\hat p=0.12` estimated proportion of people that chose chocolate​ pie

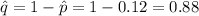`\hat q =1-\hat p=1-0.12=0.88` represent the people that NOT chose chocolate​ pie

E=0.05 represent the error or margin of error given by the following formula:

`ME=z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

z would represent the quantile of the normal standard distribution

p= true population proportion of people that chose chocolate​ pie

The confidence interval for the population proportion is given by this formula :

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

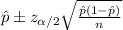
If the confidence level is 90 ​%, what is the value of alpha ​?

On this case the value for the significance would be
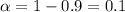`\alpha=1-0.9 =0.1` and the value of
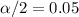`\alpha/2 =0.05`, we can find the quantiles of the normal standard distribution given by:

`z_(\alpha/2)=-1.64` and
`z_(1-\alpha/2)=1.64`

And with the following excel codes:

"=NORM.INV(0.05,0,1)" "=NORM.INV(1-0.05,0,1)"

And we can find the margin of error like this:

`ME=1.64 \sqrt{(0.12(1-0.12))/(500)}=0.0238`