Question

Use the general slicing method to find the volume of the following solids. The solid whose base is the region bounded by the curves y=x² and y=2−x², and whose cross sections through the solid perpendicular to the x-axis are squares

Answer 1

The volume is
`V=(64)/(15)`

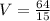
Explanation:

The General Slicing Method is given by

Suppose a solid object extends from x = a to x = b and the cross section of the solid perpendicular to the x-axis has an area given by a function A that is integrable on [a, b]. The volume of the solid is

`V=\int\limits^b_a {A(x)} \, dx`

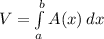
Because a typical cross section perpendicular to the x-axis is a square disk (according with the graph below), the area of a cross section is

The key observation is that the width is the distance between the upper bounding curve
`y = 2 - x^2` and the lower bounding curve
`y = x^2`

The width of each square is given by

`w=(2-x^2)-x^2=2-2x^2`

This means that the area of the square cross section at the point x is

`A(x)=(2-2x^2)^2`

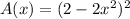
The intersection points of the two bounding curves satisfy
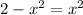`2 - x^2=x^2`, which has solutions x = ±1.

`2-x^2=x^2\\-2x^2=-2\\(-2x^2)/(-2)=(-2)/(-2)\\x^2=1\\\\x=√(1),\:x=-√(1)`

Therefore, the cross sections lie between x = -1 and x = 1. Integrating the cross-sectional areas, the volume of the solid is

`V=\int\limits^(1)_(-1) {(2-2x^2)^2} \, dx\\\\V=\int _(-1)^14-8x^2+4x^4dx\\\\V=\int _(-1)^14dx-\int _(-1)^18x^2dx+\int _(-1)^14x^4dx\\\\V=\left[4x\right]^1_(-1)-8\left[(x^3)/(3)\right]^1_(-1)+4\left[(x^5)/(5)\right]^1_(-1)\\\\V=8-(16)/(3)+(8)/(5)\\\\V=(64)/(15)`