Question

The mean gross annual incomes of certified welders are normally distributed with the mean of $20,000 and a standard deviation of $2,000. The ship building association wishes to find out whether their welders earn more or less than $20,000 annually. The alternate hypothesis is that the mean is not $20,000. If the level of significance is 0.10, what is the critical value?

1.65
1.28
±1.28
±1.65

Answer 1

Z=±1.65

Explanation:

Some previous concepts

The p-value is the probability of obtaining the observed results of a test, assuming that the null hypothesis is correct.

A z-test for one mean "is a hypothesis test that attempts to make a claim about the population mean(μ)".

The null hypothesis attempts "to show that no variation exists between variables or that a single variable is no different than its mean"

The alternative hypothesis "is the hypothesis used in hypothesis testing that is contrary to the null hypothesis"

System of hypothesis

Null hypothesis:
`\mu=20000`

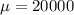
Alternative hypothesis:
`\mu \\eq 20000`

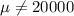
If the random variable is distributed like this:
`X \sim N(\mu=20000,\sigma=2000)`

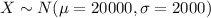
The significance level provided is
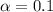`\alpha=0.1` and the value of
`\alpha/2= 0.05`.

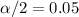Since we are conducting a bilateral test, then we have two critical values. We need to find two quantiles that accumulates 0.05 of the area on the tails of the normal standard distribution. And in order to find it we can use the following excel codes:

"=NORM.INV(0.05,0,1)" , "=NORM.INV(1-0.05,0,1)"

And we got this:

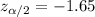`z_(\alpha/2)=-1.65` and
`z_(1-\alpha/2)=1.65`

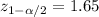
So the correct answer for this case is:

Z=±1.65