Question

Professor Elderman has given the same multiple-choice final exam in his Principles of Microeconomics class for many years. After examining his records from the past 10 years, he finds that the scores have a mean of 76 and a standard deviation of 12. What is the probability that a class of 15 students will have a class average greater than 70 on Professor Elderman’s final exam? You Answered 0.6915 Correct Answer Cannot be determined. 0.0262 0.9738

Answer 1

Answer: 0.9738

Explanation:

We assume that the scores follows a normal distribution.

Let
`\overline{x}` denotes the class average .

As per given we have,

`\mu=76\ \ \&\ \ \sigma=12`

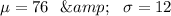
Sample size : n= 12

The probability that a class of 15 students will have a class average greater than 70 on Professor Elderman’s final exam will be :

`P(\overline{x}>70)=1-P(\overline{x}<70)\\\\=1-P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(70-76)/((12)/(√(15))))\\\\\approx1-P(z<-1.94)\ \ \ [\because\ z=\overline{x}-\mu}{(\sigma)/(√(n))}]\\\\ =1-(1-P(z<1.94))\ \ [\because P(Z<-z)=1-P(Z<z)]\\\\=1-1+P(z<1.94)\\\\=0+0.9738=0.9738\ \ \text{[By z-table]}`

Hence, the correct answer = 0.9738