Answer:
The coordinates of point P is 6 , 1
Explanation:
Given as :
The point P lies on directed line segment from points A and B
A = (
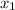 ,
,
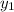 ) = (2 ,3)
) = (2 ,3)
B = (
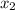 ,
,
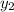 ) = (8 , 0)
) = (8 , 0)
The partitions segments in the ratio = m : n = 22 : 11
Let the coordinate of point P = x , y
Now, According to question
x =
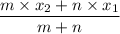
y =
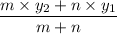
Now
x =
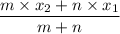
Or, x =
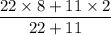
Or, x =
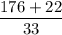
Or, x =
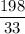
∴ x = 6
Again
y =
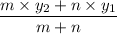
Or, y =
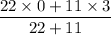
Or, y =
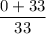
Or, y =
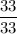
∴ y = 1
So, The coordinates of point P = x , y = 6 , 1
Hence, The coordinates of point P is 6 , 1 Answer