Answer:
Length, l = 11 ft.
Width, w = 9 ft.
Explanation:
From the given data, the area of the rectangle = 99 ft².
Area of the rectangle = Length, l X Width, w
Here, Length, l = 7 more than twice the width
⇒ Length, l = 7 + 2w
Therefore, Area, A = 99 = (7 + 2w)w
⇒ 99 = 7w + 2w²
⇒ 2w² + 7w - 99 = 0
Solve the Quadratic equation using the formula: x =
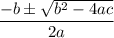 for the quadratic equation ax² + bx + c = 0.
for the quadratic equation ax² + bx + c = 0.
Therefore, w =
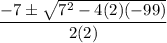
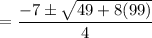
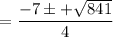
Since,
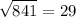 we get:
we get:

This gives two values of 'w', viz., w =
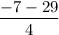 ,
,
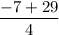
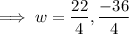
⇒ w =
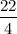 , -9.
, -9.
We take the integer values.
If w = -9, then l = 2(-9) + 7
⇒ l = - 18 + 7 = - 11
Therefore, the length, l of the rectangle = - 11 ft.
and the width, w of the rectangle = - 9 ft.
Hence, the answer.