Question

A boat travels 12 Mph in still water. It can travel 18 miles upstream in the same time that it can travel 24 miles downstream. What is the current?

Please I need it quick.

Answer 1

Answer: The current of the water is 1.714 mph.

Answer 2

Current of the water is 1.714 mph

Solution:

Given that,

A boat travels 12 Mph in still water

It can travel 18 miles upstream in the same time that it can travel 24 miles downstream

To find: current of water

Formula to remember:

If the speed of a boat in still water is u km/hr and the speed of the stream is v km/hr, then:

Speed downstream = (u + v) km/hr

Speed upstream = (u - v) km/hr

Let "t" be the time taken for upstream and downstream

Let "x" be the speed of stream or current

For upstream:

distance = 18 miles

time taken = t

speed in still water = 12 mph

speed of stream = "x"

we know that :
`speed = (distance)/(time)`

`12 - x = (18)/(t) ---- eqn 1`

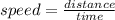
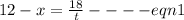
For downstream:

distance = 24 miles

time taken = t

speed in still water = 12 mph

speed of stream = "x"

`12 + x = (24)/(t) ---- eqn 2`

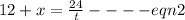
Now, adding those two equations (1) and (2) we get,

`12 - x + 12 + x = (18)/(t) + (24)/(t)\\\\24 = (18)/(t) + (24)/(t)\\\\24t = 18 + 24\\\\24t = 42\\\\t = (42)/(24)\\\\t = (7)/(4)`

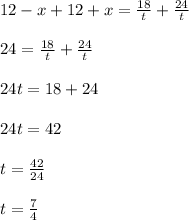
t = 1.75 hours

Now, from equation (1) we get

`12 - x = (18)/(1.75)\\\\12 - x = 10.29\\\\x = 12 - 10.29\\\\x = 1.71`

Thus current of the water is 1.71 mph