Question

Uranus moves in an elliptical orbit with the sun at one of the foci. The length of the half of the major axis is 2,876,769,540 kilometers, and the eccentricity is 0.0444. Find the minimum distance (perihelion) of Uranus from the sun. Round your answer to nearest kilometer.

Answer 1

The minimum distance (perihelion) of Uranus from the sun is 2,749,040,972.

Explanation:

Consider the provided information.

The length of the half of the major axis is 2,876,769,540 kilometers, and the eccentricity is 0.0444.

The eccentricity (e) of an ellipse is the ratio of the distance from the center to the foci (c) and the distance from the center to the vertices (a).

`e=(c)/(a)`

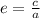
Substitute a = 2,876,769,540 and e = 0.0444 in above formula and solve for c.

`0.0444=(c)/(2,876,769,540 )`

`c=127728567.576`

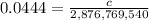
Minimum distance of Uranus from the sun is:

`a-c=2,876,769,540-127728567.576\\a-c=2749040972.424\approx2749040972`

Hence, the minimum distance (perihelion) of Uranus from the sun is 2,749,040,972.