Question

Use the population growth model. It is observed that a certain bacteria culture has a relative growth rate of 12% per hour, but in the presence of an antibiotic the relative growth rate is reduced to 5% per hour. The initial number of bacteria in the culture is 22. Find the projected population after 24 hours for the following conditions. (a) No antibiotic is present, so the relative growth rate is 12%. (b) An antibiotic is present in the culture, so the relative growth rate is reduced to 5%.

Answer 1

Part (A) The projected population after 24 hours when no antibiotic is present is 392 bacteria.

Part (B) The projected population after 24 hours when an antibiotic is present in the culture is 73 bacteria.

Explanation:

Consider the provided information.

The initial number of bacteria in the culture is 22. The projected population after 24 hours for the following conditions. Bacteria culture has a relative growth rate of 12% per hour,

Use exponential model:
`n(t)=n_0e^(rt)`

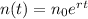
Part (A) No antibiotic is present, so the relative growth rate is 12%.

The initial number of bacteria in the culture is 22.

That means
`n(0)=22`

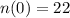
The growth rate is 12%=0.12

Times is 24 hours

Substitute the respective values in exponential model:

`n(t)=22e^(0.12* 24)`

`n(t)=391.91\approx 392`

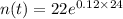
The projected population after 24 hours when no antibiotic is present is 392 bacteria.

Part (B) An antibiotic is present in the culture, so the relative growth rate is reduced to 5%.

The initial number of bacteria in the culture is 22.

That means
`n(0)=22`

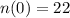
The growth rate is reduced to 5%=0.05

Times is 24 hours

Substitute the respective values in exponential model:

`n(t)=22e^(0.05* 24)`

`n(t)=73.04\approx 73`

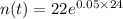
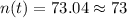
The projected population after 24 hours when an antibiotic is present in the culture is 73 bacteria.