Question

A quadilateral has diagonals represented by y=2x+5 and x+2y= -8. What is true about the quadrilateral? Please explain.

(Please do not give out a flat out answer without explaining, spam, or lie. I really want to understand this topic. Thank you!)

Answer 1

The quadrilateral has diagonals which are perpendicular to each other.

Explanation:

The equations of the diagonals are given, as

`y = 2x+5` and
`x = 2y -8`.

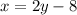The second equation can be written as,

`y = (-x-8)/(2) = (-x)/(2)-4`

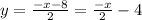
The slope of the first line is m1 = 2 and slope of second line is m2 =
`(-1)/(2)`.

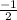Multiplying the two slopes, we get,

= (m1)(m2) =
`(2)((-1)/(2)) = -1`

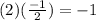
In coordinate geometry, when slopes of two lines are perpendicular, their slopes product is -1.

Thus, above two lines are perpendicular.

Thus the quadrilateral can be Rhombus,Square or Kite.