Question

1. Using n, n+1, and n+2 to represent three consecutive integers, write the statement of multiplying three consecutive integers and then adding the middle integer to the result of the multiplication as an expression.

2. Simplify the expression from problem 1 and write the answer in standard form.
3. Show that the answer from problem 2 is equivalent to the cube of the middle integer.

Answer 1

1) Expression is

`(n+1)+(n^3+3n^2+2n)=n^3+3n^2+3n+1`

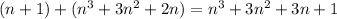
2) The standard form of the expression is

`n^3+3n^2+3n+1=(n+1)^3`

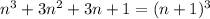
3) The expression is

`n^3+3n^2+3n+1=(n+1)^3`

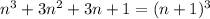
Where
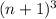`(n+1)^3` is the cube of the middle integer

Explanation:

1) Given three consecutive integers are n. n+1, and n+2

Now multiplying the three consecutive integers

`(n)(n+1)(n+2)=(n^2+n)(n+2)`

`=n^3+2n^2+n^2+2n`

`=n^3+3n^2+2n`

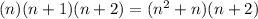
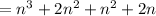
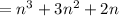
Therefore
`(n)(n+1)(n+2)=n^3+3n^2+2n`

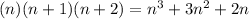
Now adding the middle integer to the result of the multiplication.

ie, adding (n+1) to the result of the multiplication
`n^3+3n^2+2n`

`(n+1)+(n^3+3n^2+2n)=n+1+n^3+3n^2+2n`

`=3n+1+n^3+3n^2`

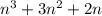
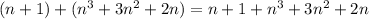
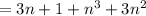
Therefore
`(n+1)+(n^3+3n^2+2n)=n^3+3n^2+3n+1`

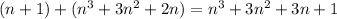
2) Expression is
`n^3+3n^2+3n+1`

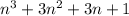
Now we simplify the above expression

`n^3+3n^2+3n+1=n^3+3n^2(1)+3(n)(1)^2+1^3`

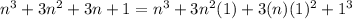
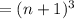`=(n+1)^3` (by using
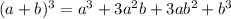`(a+b)^3=a^3+3a^2b+3ab^2+b^3` , Here a = n and b=1)

`n^3+3n^2+3n+1=(n+1)^3`

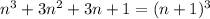
3) The expression is

`n^3+3n^2+3n+1=(n+1)^3`

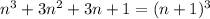
Where
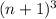`(n+1)^3` is the cube of the middle integer.

ie, expression is equivalent to the cube of the middle integer