Question

A particle with a positive charge q is moving in the positive x direction with velocity of magnitude v0. If there were an electric field in the positive y direction with magnitude E0, and the velocity of the particle is unchanged, find the magnitude and direction of magnetic field.

Answer 1

The magnitude of the magnetic field in the given scenario is zero.

Step-by-step explanation:

The magnitude and direction of the magnetic field can be determined by analyzing the force experienced by the positively charged particle q as it moves in the positive x direction and encounters an electric field in the positive y direction. The force experienced by the particle, due to the Lorentz force law, is given by:

F = qvB sin

Where F is the force, q is the charge, v is the velocity, B is the magnetic field, and θ is the angle between the velocity and the magnetic field. Since the velocity of the particle remains unchanged, the force experienced by the particle in the y direction must be zero. This means that the angle θ between the velocity and the magnetic field must be 90 degrees. Therefore, sin θ = 1. Substituting these values into the equation, we get

0 = qv0

Solving for B, we find that

B = 0

Therefore, the magnitude of the magnetic field in this scenario is zero.

Answer 2

First, let's define the coordinate axes: positive x direction is to the right, positive y direction is to upwards, and z direction is out-of-the plane (towards you).

If the particle is moving with velocity
`v_0` in the presence of an external E-field, than according to the below formula E-field pushes the positive charge in the direction of the field, which is upward.

`F = Eq`.

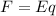If the velocity of the particle is unchanged, this means that the particle does not have an acceleration, so net force applied to the particle is zero.

We know that the force caused by the E-field is upwards, so an equal amount of another force is directed downwards. This second force is caused by magnetic field.
`|F_B| = qvB`

`F_(net) = 0\\F_(net) = F_E - F_B\\0 = qE_0 - qvB\\qE_0 = qvB\\B = (E_0)/(v)`

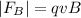
This is the magnitude of the magnetic field.

For the direction of the magnetic field we can use right-hand rule with the following equation:

`F_B = q(v * B)`

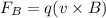
Here,
`v` is in the x-direction.
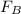`F_B` is in the (-y)-direction.

According to the right-hand rule, B-field should be in the z-direction (out-of-the plane, towards you.)

Step-by-step explanation: