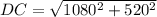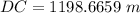Answer:
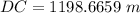
Step-by-step explanation:
Refer the schematic for explanation.
According to the given condition the first cyclist covers 1080 meters eastwards and then travels 1430 meters northwards to reach the camp.
But the second cyclist travels 1950 meters northwards therefore he travelled 520 meters more in the north than the first cyclist.
So, according to the schematic we find the distance DC in the triangle DCE using Pythagoras theorem: