Answer:
The sum of first 9 terms of the given sequence = 68887
Explanation:
Given sequence:
7+21+63......
The given sequence is a geometric sequence as the successive numbers bear a common ratio.
The ratio can be found out by dividing a number by the number preceding it.
For the given geometric sequence common ratio
 can be given as:
can be given as:
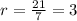
The sum of a geometric sequence is given by:
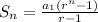 when
when
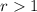
and
 when
when
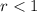
where,
 represents sum of
represents sum of
 terms,
terms,
 representing number of terms and
representing number of terms and
 represents common ratio and
represents common ratio and
 represents the first term.
represents the first term.
Since for the given geometric sequence has a common ratio =3 which is >1, so we will use the first formula for sum to calculate the sum of first 9 terms.
Plugging in the values to find sum of first 9 terms.
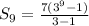
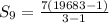
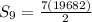
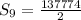
∴

Thus sum of first 9 terms of the given sequence = 68887 (Answer)