Question

Which function has a vertex at the origin?

O f(x) = (x + 4)
O f(x) = x(x – 4)
O f(x) = (x – 4)(x + 4)
O f(x) = 2

Answer 1

B)
`f(x)=x(x-4)`

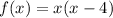
Explanation:

To find the function which has vertex at the origin.

Solution:

For a function to have its vertex at origin the function must pass through point (0,0) which means
`f(0)=0`.

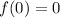We will find
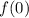`f(0)` for each of the given functions and check if it has vertex at origin.

To find
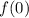`f(0)` we will plugin
`x=0` in the function.

A)
`f(x)=x+4`

`f(0)=0+4=4`

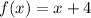
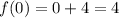
Vertex is not at the origin.

B)
`f(x)=x(x-4)`

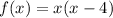
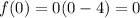`f(0)=0(0-4)=0` [Any number times zero is = zero]

Vertex is at the origin.

C)
`f(x)=(x-4)(x+4)`

`f(0)=(0-4)(0+4)=(-4)(4)=-16`

Vertex is not at the origin.

D)
`f(x)=2`

`f(0)=2`

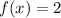
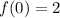
Vertex is not at the origin.