Question

30 points

1)The function g is defined by g(x)=cx−3, where c is a constant. Find c, if the value of g(x) at x=0.5 is equal to −1.
2)The function h is defined by h(x)=(20x−k)÷x+50, where k is a constant. Find k, if the value of ℎ at x=20 is equal to 65.

Answer 1

1) The value of c is given by

`c=4`

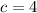
2) The value of k is given by

`k=-4150`

Explanation:

Given that function g is defined by
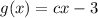`g(x)=cx-3` , where c is a constant.

To find c:

Also given that value of g(x) at x=0.5 is equal to -1

ie.,
`g(0.5)=-1`

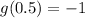
At x=0.5

`g(0.5)=c(0.5)-3=-1`

`(0.5)c-3=-1`

`(0.5)c=-1+3`

`(0.5)c=2`

`c=(2)/(0.5)`

`c=\frac{2}{\tfrac{1}{2}}=2* (2)/(1)`

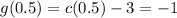
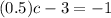
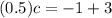
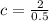
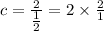
Therefore
`c=4`

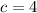
2) Given that function h is defined by
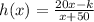`h(x)=(20x-k)/(x+50)` , where k is a constant.

To find k:

Also given that value of h(x) at x=20 is equal to 65

ie.,
`h(20)=65`

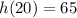
At x=20

`h(20)=(20(20)-k)/(20+50)=65`

`400-k=65(70)`

`-k=4550-400`

`-k=4150`

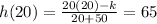
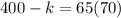
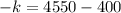
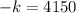
Therefore
`k=-4150`