Question

Word problem : There are 850 Douglas Fir and Ponderosa pine trees in a section of the forest bought by karamazov logging co. The company paid an average of $300 for each Douglas for and $225 for each Ponderosa pine. If the company paid an average of 217,500 trees, how many of each did the company buy?

Answer 1

The company bought 350 Douglas Fir bought and 500 Ponderosa pine trees bought

Solution:

Let "d" be the number of Douglas Fir bought

Let "p" be the number of Ponderosa pine trees bought

Cost of 1 douglas fir = $ 300

Cost of 1 ponderosa pine = $ 225

Given that There are 850 Douglas Fir and Ponderosa pine trees in a section of the forest bought by karamazov logging co

So we can frame a equation as:

number of Douglas Fir bought + number of Ponderosa pine bought = 850

d + p = 850 --- eqn 1

Given that the company paid an average of 217,500 trees

So we frame a equation as:

number of Douglas Fir bought x Cost of 1 douglas fir + number of Ponderosa pine trees bought x Cost of 1 ponderosa pine = 217500

`d * 300 + p * 225 = 217500`

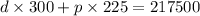
300d + 225p = 217500 --- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "d" and "p"

From eqn 1,

d = 850 - p --- eqn 3

Substitute eqn 3 in eqn 2

300(850 - p) + 225p = 217500

255000 - 300p + 225p = 217500

-75p = 217500 - 255000

-75p = -37500

p = 500

Substitute p = 500 in eqn 3

d = 850 - 500

d = 350

Thus the company bought 350 Douglas Fir bought and 500 Ponderosa pine trees bought