Question

The half-life of a substance is how long it takes for half of the substance to decay or become harmless (for certain radioactive materials). The half-life of a substance is 37 years and there is an amount equal to 202 grams now. What is the expression for the amount A(t) that remains after t years, and what is the amount of the substance remaining (rounded to the nearest tenth) after 100 years?

Answer 1

31.0 grams.

Explanation:

According to the given information

Half-life of a substance = 37 years

Initial amount = 202 gram

The exponential function for half-life of a substance is

`A(t)=A_0(0.5)^{(t)/(h)}`

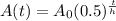
where, A₀ is initial amount, t is time and h is half life.

Substitute A₀=202 and h=37 in the above function.

`A(t)=202(0.5)^{(t)/(37)}`

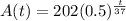
We need to find the amount of the substance remaining after 100 years.

Substitute t=100 in the above function.

`A(100)=202(0.5)^{(100)/(37)}`

`A(100)=31.0282146`

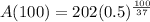
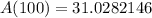
Round the answer to the nearest tenth.

`A(100)\approx 31.0`

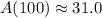
Therefore, the amount of the substance remaining after 100 years is 31.0 grams.