Answer:
Torque,
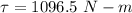
Step-by-step explanation:
It is given that,
Mass of the merry go round, m = 357 kg
Radius of the horizontal disk, r = 2 m
Initial speed of the merry go round,
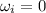
Final angular speed,
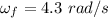
Time, t = 2.8 s
It is set in motion by wrapping a rope about the rim of the disk and pulling on the rope. We need to find how large a torque would have to be exerted to bring the merry-go-round from rest to an angular speed of 4.3 rad/s in 2.8 s. It is given by :
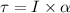
I is the moment of inertia of the disk,
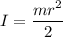
 is the angular acceleration
is the angular acceleration
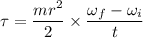

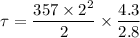
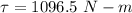
So, the torque exerted is 1096.5 N-m. Hence, this is the required solution.