Question

The mass percent of carbon in a typical human is 18%, and the mass percent of 14C in natural carbon is 1.6 × 10-10%. Assuming a 190.-lb person, how many decay events per second occur in this person due exclusively to the β-particle decay of 14C? For 14C, t1/2 = 5730 years

Answer 1

4066 decay/s

Step-by-step explanation:

Given that:-

The weight of the person is:- 190 lb

Also, 1 lb = 453.592 g

So, weight of the person = 86182.6 g

Also, given that carbon is 18% in the human body. So,

`\%\ Carbon=(18)/(100)* 86182.6\ g=15512.868\ g`

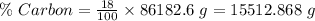
Carbon-14 is
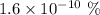`1.6* 10^(-10)\ \%` of the carbon in the body. So,

`\%\ Carbon-14=(1.6* 10^(-10))/(100)* 15512.868\ g=2.48* 10^(-8)\ g`

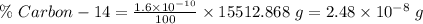
Also,

14 g of Carbon-14 contains
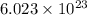`6.023* 10^(23)` atoms of carbon-14

So,

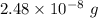`2.48* 10^(-8)\ g` of Carbon-14 contains
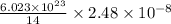`(6.023* 10^(23))/(14)* 2.48* 10^(-8)` atoms of carbon-14

Atoms of carbon-14 =
`1.07* 10^(15)`

Given that:

Half life = 5730 years

`t_(1/2)=\frac {ln\ 2}{k}`

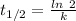
Where, k is rate constant

So,

`k=\frac {ln\ 2}{t_(1/2)}`

`k=(ln\ 2)/(5730)\ years^(-1)`

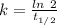
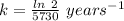
The rate constant, k = 0.00012 years⁻¹

Also, 1 year =
`3.154* 10^7` s

So, The rate constant, k =
`(0.00012)/(3.154* 10^7)` s⁻¹ =
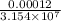`3.8* 10^(-12)\ s^(-1)`

Thus, decay events per second =
`K* atoms decayed` =
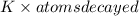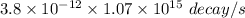`3.8* 10^(-12)* 1.07* 10^(15)\ decay/s` = 4066 decay/s