Question

The number of "destination weddings" has skyrocketed in recent years. For example, many couples are opting to have their weddings in the Caribbean. A Caribbean vacation resort recently advertised in Bride Magazine that the cost of a Caribbean wedding was less than $30,000. Listed below is a total cost in $000 for a sample of 8 Caribbean weddings.

29.1 28.5 28.8 29.4 29.8 29.8 30.1 30.6
1. At the 0.05 significance level, is it reasonable to conclude the mean wedding cost is less than $30,000 as advertised?
2. State the null hypothesis and the alternate hypothesis. Use a 0.05 level of significance. (Enter your answers in thousands of dollars.)

Answer 1

There is no sufficient evidence to support the claim that wedding cost is less than $30000.

Explanation:

Values (x) ∑(Xi-X)^2

----------------------------------

29.1 0.1702

28.5 1.0252

28.8 0.5077

29.4 0.0127

29.8 0.0827

29.8 0.0827

30.1 0.3452

30.6 1.1827

----------------------------------------

236.1 3.4088

Mean = 236.1 / 8 = 29.51

`S_(x)=√(3.4088/(8-1))=0.6978`

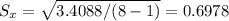
Statement of the null hypothesis:

H0: u ≥ 30 the mean wedding cost is not less than $30,000

H1: u < 30 the mean wedding cost is less than $30,000

Test Statistic:

`t=(X-u)/(S/√(n))=(29.51-30)/(0.6978/√(8))= (-0.49)/(0.2467)=-1.9861`

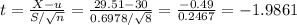
Test criteria:

SIgnificance level = 0.05

Degrees of freedom = df = n - 1 = 8 - 1 = 7

Reject null hypothesis (H0) if

`t<-t_(0.05,n-1)\\ t<-t_(0.05,8-1)\\ t<-t_(0.05,7)`

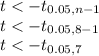
Finding in the t distribution table α=0.05 with df=7, we have

`t_(0.05,7)=2.365`

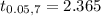
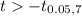`t>-t_(0.05,7)` = -1.9861 > -2.365

Result: Fail to reject null hypothesis

Conclusion: Do no reject the null hypothesis

u ≥ 30 the mean wedding cost is not less than $30,000

There is no sufficient evidence to support the claim that wedding cost is less than $30000.

Hope this helps!