Answer:
Therefore the value of x in the triangle is 61.9°.
Explanation:
Given:
Consider In Right Angle Triangle ABC
∠B = 90°
∠A = x°
AB = 8 = adjacent side of 'x'
BC = 15 = opposite side of 'x'
To Find:
x = ?
Solution:
In Right Angle Triangle ABC by Tangent Identity we have
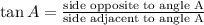
substituting the above given values we get
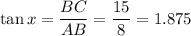

Therefore the value of x in the triangle is 61.9°.