Question

Gravitational force of attraction “F” exists between two point masses A and B when a fixed distance separates them. After mass A is tripled and mass B is halved, the gravitational attraction between the two masses is

1/6 F
2/3 F
3/2 F
6 F

Answer 1

3/2 F is the Answer

Answer 2

the new gravitational force between the two masses is
`(3)/(2)` of the original force (third option in the provided list)

Step-by-step explanation:

Recall the expression for gravitational force :
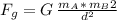`F_g=G\,(m_A*\,m_B2)/(d^2)`, where
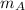`m_A` and
`m_B` are the point masses, d the distance between them, and G the universal gravitational constant.

I our problem, the distant between the particles stays unchanged, and we need to know what happens with the magnitude of the force as mass A is tripled, and mass B is halved.

Initial force expression:
`F_i=G\,(m_A\,m_B)/(d^2)`

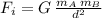
Final force expression:
`F_f=G\,(3*m_A\,m_B/2)/(d^2)\\F_f=G\,(m_A\,m_B\,*\,3/2)/(d^2)\\F_f=G\,(m_A\,m_B)/(d^2)\,*(3)/(2) \\F_f=F_i\,*(3)/(2)`

Where we have recognized the expression for the initial force between the particles, and replaced it with
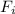`F_i` to make the new relation obvious.

Therefore, the new gravitational force between the two masses is
`(3)/(2)` of the original force.