Question

Assume that a simple random sample has been selected from a normally distributed population and test the given claim. Identify the null and alternative hypotheses, test statistic, P-value, critical value(s). and state the final conclusion that addresses the original claim. A safety administration conducted crash tests of child booster seats for cars. Listed below are results from those tests, with the measurements given in hie (standard head injury condition units). The safety requirement is that the hic measurement should be less than 1000 hic. Use a 0.05 significance level to test the claim that the sample is from a population with a mean less than 1000 hic. Do the results suggest that all of the child booster seats meet the specified requirement? 697 759 1266 621 569 432

What are the hypotheses

Identify the test statistic

Identify the P-value.

The critical value(s) is(are)

State the final conclusion that addressses the original claim

What do the results suggest about the child booster seats eeting the specific requirement?

Answer 1

There is sufficient evidence to conclude that child booster seats meet the specific requirement.

Explanation:

Sample: 697, 759, 1266, 621, 569, 432

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(4344)/(6) = 724`

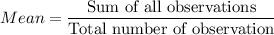
Sum of squares of differences = 415616

`S.D = \sqrt{(415616)/(5)} = 288.31`

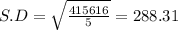
We are given the following in the question:

Population mean, μ = 1000 hic

Sample mean,
`\bar{x}` = 724

Sample size, n = 16

Alpha, α = 0.05

Sample standard deviation, s = 288.31

First, we design the null and the alternate hypothesis

`H_(0): \mu = 1000\text{ hic}\\H_A: \mu < 1000\text{ hic}`

We use one-tailed(left) t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

Putting all the values, we have

`t_(stat) = \displaystyle(724 - 1000)/((288.31)/(√(6)) ) = -2.344`

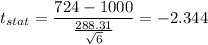
Now,
`t_(critical) \text{ at 0.05 level of significance, 5 degree of freedom } = -2.015`

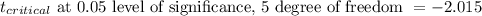
Calculation the p-value from table,

P-value = 0.033

Since,

Since, the p value is lower than the significance level, we fail to accept the null hypothesis and reject it. We accept the alternate hypothesis.

We conclude that the measurement is less than 1000 hic.

Thus, there is sufficient evidence to conclude that child booster seats meet the specific requirement.