Question

Which of the following is the quotient of the complex numbers below ?

(10+2i)/(5-6i)

Answer 1

`$ (38)/(61) + (70)/(61)i $`

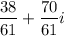
Explanation:

Given:
`$ (10 + 2i)/(5 - 6i) $`

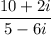
We multiply both the numerator and denominator by the complex conjugate of the denominator.

We have:

`$ (10 + 2i)/(5 - 6i) = (10 + 2i)/(5 - 6i) * (5 + 6i)/(5 + 6i) $`

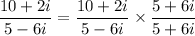
This equals
`$ ((10 - 2i)(5 - 6i))/((5 - 6i)(5 + 6i)) $`

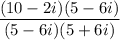
Note that the denominator is of the form,
`$ (a + ib)(a - ib) $`.

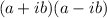This is equal to
`$ a^2 + b^2 $`.

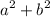Multiplying the numerator term - wise and applying the above formula for denominator, we have:

`$ ((10 + 2i)(5 + 6i))/(5^2 + 6^2) $`

`$ (50 + 60i + 10i - 12)/(61) $`

`$ = (38 + 70i)/(61) $`

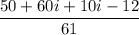
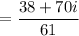
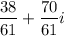`$ (38)/(61) + (70)/(61)i $` is the required answer.