Question

A person of mass 70 kg stands at the center of a rotating merry-go-round platform of radius 2.7 m and moment of inertia 890 kg⋅m2 . The platform rotates without friction with angular velocity 0.85 rad/s . The person walks radially to the edge of the platform. Part APart complete Calculate the angular velocity when the person reaches the e

Answer 1

Step-by-step explanation:

Using the Condition That Initial Angular Velocity is equal to final angular velocity

total angular momentum is equal to angular momentum of the person + angular Momentum of the Platform
`L_(T) = L_(plat) + L_(per)`

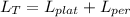
Note L= I ×ω

Final Angular momentum of the person is equal to the final angular momentum of the platform

Final Moment of Inertia of the person I_{per.f} =
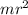`mr^(2)` =70×(2.7)²=510.3Kgm2

Initial Angular Momentum L_{i} = Final Angular Momentum L_{f}

I_{plat.i} ×ω_{plat.i} + I_{per.i} ×ω_{per.i} = I_{plat.f} ×ω_{plat.f} + I_{per.f} ×ω_{per.f}

890(0.85) + 0 =890(ω_{plat.f}) +510.3(ω_{plat.f})

756.5 = 1400.3 (ω_{plat.f})

(ω_{plat.f}) =0.54rad/s