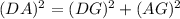Answer:
Therefore, Michael concludes option C)
C)
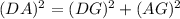
Explanation:
Given:
1. DG = 3 and the area of square DEFG is 9.
2. AG = 4 and the area of square GHIA is 16.
3. DA = 5 and the area of square ABCD is 25.
So we have,
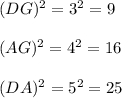
Now Add DG² and AG² we get
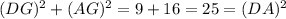
Which is also called as Pythagoras theorem i.e
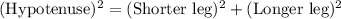
Therefore, Michael concludes option C)
C)