Answer:
If Discriminant,
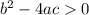
Then it has Two Real Solutions.
Explanation:
To Find:
If discriminant (b^2 -4ac>0) how many real solutions
Solution:
Consider a Quadratic Equation in General Form as
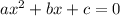
then,
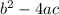 is called as Discriminant.
is called as Discriminant.
So,
If Discriminant,
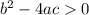
Then it has Two Real Solutions.
If Discriminant,
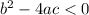
Then it has Two Imaginary Solutions.
If Discriminant,
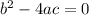
Then it has Two Equal and Real Solutions.