Question

The perimeter of a rectangle is represented by

2
4x. + 5x -2. The perimeter of a smaller rectangle is represented 2
by x. +3x+5 which polynomial expression BEST represents how much larger the first rectangle is the smaller rectangle

Answer 1

The perimeter of a rectangle is represented by 4x^2 + 5x − 2. The perimeter of a smaller rectangle is represented by x^2 + 3x + 5. Which polynomial expression BEST represents how much larger the first rectangle is than the smaller rectangle?

A) 3x^2 + 2x − 7

B) 3x^2 + 2x − 3

C) 3x^2 + 8x + 3

D) 5x^2 + 8x − 7

Answer:

Option A

The polynomial expression best represents how much larger the first rectangle is than the smaller rectangle is
`3 x^(2)+2 x-7`

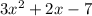
Solution:

Perimeter of a rectangle is represented by 4x^2 + 5x − 2

Perimeter of a smaller rectangle is represented by x^2 + 3x + 5

To Find : Polynomial expression that represents how much larger the first rectangle is than the smaller rectangle.

Which means we have to find difference between perimeter of both rectangles

Subtract the equation of perimeter of smaller rectangle from equation of perimeter of a larger rectangle

Difference = perimeter of a larger rectangle - perimeter of smaller rectangle

`\text {Difference }=\left(4 x^(2)+5 x-2\right)-\left(x^(2)+3 x+5\right)`

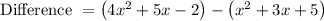
On removing the brackets we get,

`\begin{array}{l}{\text { Difference }=4 x^(2)+5 x-2-x^(2)-3 x-5} \\\\ {\text { Difference }=3 x^(2)+2 x-7}\end{array}`

Thus option A is correct