Answer:
the highest value of the Paschen series is 18805 μm which is greater than the shortest value of the Brackett series (14617 μm).
Step-by-step explanation:
Hydrogen atom transitions are described by the Bohr model
 = -13.606 / n²
= -13.606 / n²
Where n is an integer
Transitions occur between two states with different quantum numbers n
ΔE = -13.606 (1 /
 ² - 1 /
² - 1 /
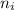 ²)
²)
Where
 >
>
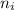
For the wavelength we use the Planck equation
E = h f
c = λ f
E = h c / λ
λ = h c / E
λ = 6.63 10⁻³⁴ 3 10⁸ / E
λ = 19.89 10⁻²⁶ / E
Let's reduce to eV
λ = 19.89 10⁻²⁶ / E[J] (Ev / 1.6 10⁻¹⁹ J)
Lam = 12430 / E [eV]
Let's calculate the energy for transitions
Paschen Series

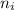 ΔE (eV) λ (um)
ΔE (eV) λ (um)
4 3 0.661 18805
5 3 0.9657 12871
10 3 1.3757 9035
100 3 1.5104 8229
∞ 3 1.5117 8222
Brackett Series

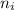 ΔE (eV) λ (um)
ΔE (eV) λ (um)
5 4 0.3061 40607
6 4 0.4724 26312
10 4 0.7143 17401
100 4 0.8490 14640
∞ 4 0.8504 14617
When we analyze the wavelength values we see that the highest value of the Paschen series is 18805 μm which is greater than the shortest value of the Brackett series (14617 μm).