Question

The demand function for a certain make of replacement cartridges for a water purifier is given by the following equation where p is the unit price in dollars and x is the quantity demanded each week, measured in units of a thousand.

p = −0.01x^2 − 0.1x + 21
1. Determine the consumers' surplus if the market price is set at $1/cartridge. (Round your answer to two decimal places.)

Answer 1

The consumer surplus is $ 506.67 when the market price is set at $1 per cartridge.

Explanation:

In order to find the Consumer Surplus we need to find first the quantity at which we have the market price.

Equilibrium quantity.

We can use the given price of $1 for each cartridge on the demand function to get

`1=-0.01x^2-0.1x+21`

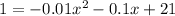
And we can move all terms to the left side.

`0.01x^2+0.1x+1-21=0\\0.01x^2+0.1x-20=0`

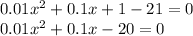
Then we can multiply all terms of both sides by 100 to get rid of the decimals.

`x^2+10x-200=0`

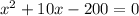
And we can work with factorization, such we need to think of what couple of numbers multiplied give us the last term, -200, but their sum must give us the middle coefficient, +10.

Those numbers are +50 and -40, so we get

`(x-50)(x+40)=0`

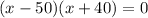
Setting each factor equal to 0.

`x = -50  \qquad and \qquad x = 40`

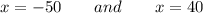
Thus the equilibrium quantity is 40 units per week.

Consumer surplus

We can use the given market price and the quantity we have found on the following equation.

`C_s =\displaystyle \int_0^(x_e) (D(x) -p_e )dx`

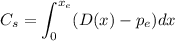
Replacing the values and equation.

`C_s =\displaystyle \int_0^(40) (-0.01x^2-0.1x+21 -1 )\,dx`

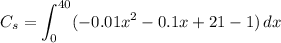
Simplifying

`C_s =\displaystyle \int_0^(40) (-0.01x^2-0.1x+20 )\,dx`

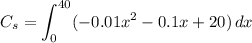
Integrating each term.

`C_s =\displaystyle \left(-\cfrac{0.01}3x^3-\cfrac{0.1}2x^2+20x \right)_0^(40)`

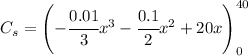
And we can evaluate at the interval.

`C_s =\displaystyle \left(-\cfrac{0.01}3(40)^3-\cfrac{0.1}2(40)^2+20(40)-\left(-\cfrac{0.01}3(0)^3-\cfrac{0.1}2(0)^2+20(0) \right) \right)`

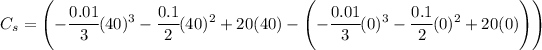
Finally arriving to

`\boxed{C_s =506.67}`

Thus consumer surplus is $ 506.67 when the market price is set at $1 per cartridge.