Question

The energy of the electron in a hydrogen atom can be calculated from the Bohr formula:

E= -Ry/n^2
In this equation, Ry stands for the Rydberg energy, and n stands for the principal quantum number of the orbital that holds the electron.
A) Calculate the wavelength of the line in the absorption line spectrum of hydrogen caused by the transition of the electron from an orbital with n=2 to an orbital with n=3 . Round your answer to significant digits.

Answer 1

`\lambda=656.34* 10^(-9)\ m`

Step-by-step explanation:

Using the Rydberg formula as:

`\frac {1}{\lambda}=R_H* (\frac {1}{n_(i)^2}-\frac {1}{n_(f)^2})`

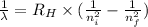
where,

λ is wavelength of photon

R = Rydberg's constant (1.097 × 10⁷ m⁻¹)

n₁ is the initial final level and n₂ is the final energy level

Given that:-

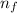`n_f` = 3

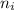`n_i` = 2

Applying in the formula as:

`(1)/(\lambda)=1.097* 10^7* ((1)/(2^2)-(1)/(3^2))`

`(1000)/(\lambda)=10970000000\left((1)/(4)-(1)/(9)\right)`

`10970000000\left((1)/(4)-(1)/(9)\right)\lambda=1000`

`\lambda=(9)/(13712500)`

`\lambda=656.34* 10^(-9)\ m`

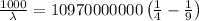
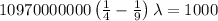
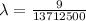
The wavelength of the line in the absorption line spectrum of hydrogen caused by the transition of the electron from an orbital with n=2 to an orbital with n=3 is:-
`656.34* 10^(-9)\ m`