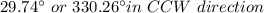Answer:
0.1040512455 N

0.05925 N
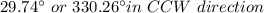
Step-by-step explanation:
I = Current
B = Magnetic field
Separation between end points is
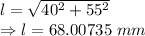
Effective force is given by
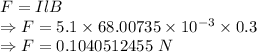
The force is 0.1040512455 N

The angle the force makes is given by

The direction is

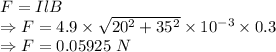
The force is 0.05925 N
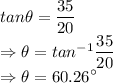

The direction is