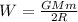Question

Calculate how much work is required to launch a spacecraft of mass m from the surface of the earth (mass mE, radius RE) and place it in a circular low earth orbit--that is, an orbit whose altitude above the earth's surface is much less than RE. (As an example, the International Space Station is in low earth orbit at an altitude of about 400 km, much less than RE = 6370 km.) Ignore the kinetic energy that the spacecraft has on the ground due to the earth's rotation.

Answer 1

To solve this problem it is necessary to apply the concepts related to the conservation of energy, through the balance between the work done and its respective transformation from the gravitational potential energy.

Mathematically the conservation of these two energies can be given through

`W = U_f - U_i`

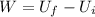
Where,

W = Work

`U_f =` Final gravitational Potential energy

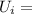`U_i =` Initial gravitational Potential energy

When the spacecraft of mass m is on the surface of the earth then the energy possessed by it

`U_i = (-GMm)/(R)`

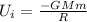
Where

M = mass of earth

m = Mass of spacecraft

R = Radius of earth

Let the spacecraft is now in an orbit whose attitude is
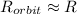`R_(orbit) \approx R` then the energy possessed by the spacecraft is

`U_f = (-GMm)/(2R)`

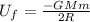
Work needed to put it in orbit is the difference between the above two

`W = U_f - U_i`

`W = -GMm ((1)/(2R)-(1)/(R))`

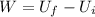
Therefore the work required to launch a spacecraft from the surface of the Eart andplace it ina circularlow earth orbit is

`W = (GMm)/(2R)`