Question

Does (1, 1) make the inequality 2x + 17y ≥ 19 true?

Answer 1

The point (1, 1) makes the inequality
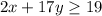`2x+17y\geq 19` true.

Explanation:

Given inequality:

`2x+17y\geq 19`

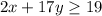
Point (1,1)

To check if the inequality is true for the given point.

Solution:

For a point
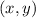`(x,y)` to make the inequality true it must lie within the inequality range, or in other words it must be a solution of the inequality.

To check if point (1,1) lies within the inequality range, we will plugin the
`x` and
`y` values of the point in the given inequality.

Plugging in
`x=1` and
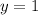`y=1` in the inequality.

`2(1)+17(1)\geq 19`

`2+17\geq 19`

`19\geq 19`

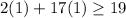
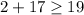
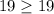
Thus it satisfies the inequality as 19 is included in the inequality.

Thus, we say point (1, 1) makes the inequality
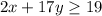`2x+17y\geq 19` true.

The graph of the inequality
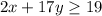`2x+17y\geq 19` and the location of the point (1,1) is shown below.