Question

Engineers and science fiction writers have proposed designing space stations in the shape of a rotating wheel or ring, which would allow astronauts to experience a sort of artificial gravity when walking along the inner wall of the station's outer rim. (a) Imagine one such station with a diameter of 121 m, where the apparent gravity is 2.60 m/s2 at the outer rim. How fast is the station rotating in revolutions per minute?

Answer 1

w = 1.976 rpm

Step-by-step explanation:

For simulate the gravity we will use the centripetal aceleration
`a_c`, so:

`a_c = w^2r`

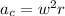
where w is the angular aceleration and r the radius.

We know by the question that:

r = 60.5m

`a_c` = 2.6m/s2

So, Replacing the data, and solving for w, we get:

`2.6m/s = w^2(60.5m)`

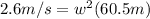
W = 0.207 rad/s

Finally we change the angular velocity from rad/s to rpm as:

W = 0.207 rad/s = 0.207*60/(2
`\pi`)= 1.976 rpm