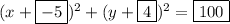Answer:
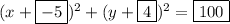
Explanation:
Given:
Center of circle is at (5, -4).
A point on the circle is
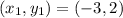
Equation of a circle with center
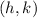 and radius 'r' is given as:
and radius 'r' is given as:

Here,
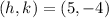
Radius of a circle is equal to the distance of point on the circle from the center of the circle and is given using the distance formula for square of the distance as:
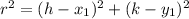
Using distance formula for the points (5, -4) and (-3, 2), we get
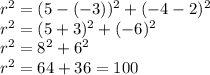
Therefore, the equation of the circle is:
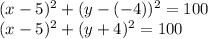
Now, rewriting it in the form asked in the question, we get