Answer:
OPTION A:
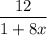 , where
, where
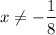 .
.
Explanation:
Given:
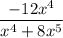
Taking
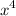 common outside in the denominator, we get:
common outside in the denominator, we get:
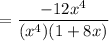
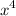 will get cancelled on the numerator and denominator, we get:
will get cancelled on the numerator and denominator, we get:
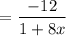
we know that the denominator can not be zero.
That means, 1 + 8x
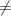 0.
0.
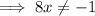
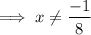
So, the answer is:
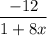 , where
, where
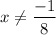 .
.