Answer:
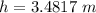
Step-by-step explanation:
Given:
- Pressure of a gas,
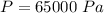
- density of the fluid in the manometer,

We know that:
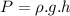
putting respective values
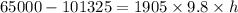
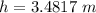 is the reading in terms of the fluid column height on the manometer.
is the reading in terms of the fluid column height on the manometer.
Considering the rise in the level of fluid this fluid is not suitable for such huge pressures for a practically convenient manometer.