Answer:
Vs = 6.73 m/s or Vs = 16.3 m/s
Step-by-step explanation:
frequency of the trains whistle (f) = 1.64 x 10^{2} Hz = 164 Hz
frequency of beats heard = 4 beats/s = 4 Hz
velocity of the stationary train (Vr) = 0
velocity of sound in air (V) = 343 m/s
velocity of the moving train (Vs) = ?
we can get the velocity of the moving train from the formula below
Fn = f x
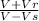 ...equation 1
...equation 1
where Fn = net frequency
- case one - assuming the train is approaching the station Fn = 164 + 4 = 168 Hz
substituting the known values into equation 1
168 = 164 x
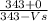
1.02 =
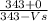
Vs =
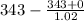
Vs = 6.73 m/s
- case two - assuming the train is leaving the station Fn = 164 - 4 = 160 Hz
substituting the known values into equation 1
168 = 160 x
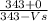
1.05 =
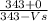
Vs =
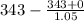
Vs = 16.3 m/s