Question

Find the length of line segment GF

right triangle E F G; angle G is a right angle; side EF has a length of 9 point 4; side EG has a length of 6 point 8

Answer 1

The length of line segment GF is 6.49 units.

Explanation:

Given:

In Right angle Triangle Δ EFG,

∠ G = 90°

EF = 9.4 = Hypotenuse (say)

EG = 6.8 = Longer Leg (say)

To Find:

GF = Shorter Leg (say)?

Solution:

In Right angle Triangle Δ EFG By Pythagoras theorem we have,

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

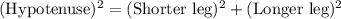
Substituting the given values we get

`9.4^(2)= l(GF)^(2)+ 6.8^(2) \\\\l(GF)^(2)=9.4^(2)- 6.8^(2) \\\\l(GF)^(2) =42.12\\\\l(GF)=6.489\\\\\therefore l(GF)=6.49`

The length of line segment GF is 6.49 units.