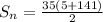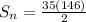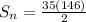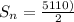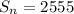Question

5. Find the sum of the first 35 terms of the arithmetic sequence when a = 5 and d = 4

Answer 1

The sum of the first 35 terms of the arithmetic sequence when a = 5 and d = 4 is 2555.

Explanation:

Given:

a = 5

d = 4

To Find :

The sum of first 35 terms of the arithmetic sequence = ?

Solution:

Step 1 : finding the 35th term

`a_n = a_1 +(n-1)d`

`a_35 = 5 +(35-1)4`

`a_35 = 5 +(34)4`

`a_35 = 5 +136`

`a_35 = 141`

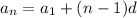
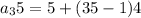
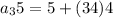
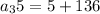
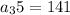
Step 2: Finding the sum of first 35 terms

`S_n = (n(a_1 +a_n))/(2)`

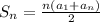
Substituting the values

`S_n = (35(5+141))/(2)`

`S_n = (35(146))/(2)`

`S_n = (35(146))/(2)`

`S_n = (5110))/(2)`

`S_n = 2555`