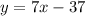Answer:
The equation of a line parallel to y = 7x - 8 that passes through (5,-2):
:
Explanation:
Given equation of the line :
y = 7x - 8
Slope intercept form = y = mx + c
Where = m = Slope of the line
c = intercept on y axis
On comparing the given equation with slope intercept form , we get
m = 7, c = -8
For equation of line which parallel to the line formed by given equation will have same slope because parallel lines have same value of slope.
m' = m= 7
Equation of the line passing from point (5,-2) can be determined by the help of point slop form;
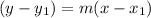
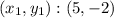
Slope of the parallel line = m' =7
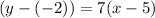
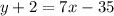
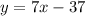
The equation of a line parallel to y = 7x - 8 that passes through (5,-2):
: