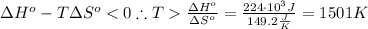Answer:
K = 0.0450, T > 1501 K
Step-by-step explanation:
We may apply the Gibbs free energy equation relating the Gibbs free energy to an equilibrium constant of a reaction. The relationship is described by the following equation:
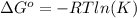
Rearrange the equation for the equilibrium constant:
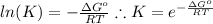
Given the temperature
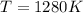 and the ideal gas law constant
and the ideal gas law constant
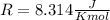 , we obtain:
, we obtain:
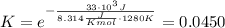
Now notice if
 , then
, then
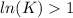 and
and
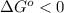 .
.
We may firstly solve for the entropy change of this reaction using the following equation:
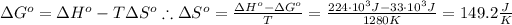
Using the same equation, solve when the change in the Gibbs free energy is negative: